Answer:
Option B is correct
The number of real number solutions for the given equation is, 1.
Explanation:
Given the equation:
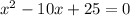
Since, this is a quadratic equation of the form of
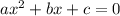
where a =1 , b = -10 and c =25.
The discriminant of a quadratic equation is,
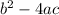
then;
Discriminant =
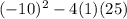 = (100-100) = 0
= (100-100) = 0
Since, a discriminant of zero means there is only one real solution for x.
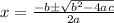
Substitute the given values.
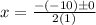
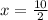
Simplify:
x = 5
Therefore, the number of real solution for the given equation is, 1