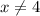A discontinuity is a point that cannot exist because the x-coordinate would cause a problem in the equation. If you have a polynomial in the denominator, you must find which values of x would cause the polynomial in the denominator to evaluate to zero. Since division by zero is undefined, that would cause a discontinuity.
Let's look at your function.


is in the numerator. It is defined for every value of x. There is no problem there.

is in the denominator. This is a function defined for every value of x, but since it is in the denominator, we must exclude the x-value that would cause this polynomial to evaluate to zero.
We set it equal to zero and solve the equation for x.
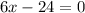
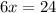
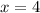
For x = 0, the denominator has a value of zero, so at this point there is a discontinuity in function f(x).
The answer is: