Question

4 times the measure of the complement of an angle is equal to 2/3 the measure of the original angle's supplement. What is the measure of the angle?.

18
48
72
108

Answer 1

Angle: x=?
Complement of the angle: y=90°-x
Supplement of the angle: z=180°-x

4 times the measure of the complement of an angle is equal to 2/3 the measure of the original angle's supplement:
4y=(2/3)z
Multiplying both sides of the equation by 3/2:
(3/2)(4y)=(3/2)(2/3)z
12y/2=(6/6)z
6y=z

Replacing y by 90°-x and z by 180°-x
6(90°-x)=180°-x

Solving for x:
540°-6x=180°-x
540°-6x+6x-180°=180°-x+6x-180°
360°=5x
5x=360°
5x/5=360°/5
x=72°

Answer: Third option 72°

Answer 2

Correct Ans:
72 °

Solution:
The angles which sum up to 90° are complementary angles. The angles which sum up to 180° are supplementary angles.

Let the unknown angle be x°. So the complement of x° will be (90 - x)°. And the supplement of x° will be (180 - x)°

According to the given data, 4 times the measure of complement of x° which is (90 - x)° is equal to 2/3 the measure of supplement of x° which is (180 - x)°. So in equation form we can write it as:


`4(90-x)= (2)/(3)(180-x) \\ \\ 12(90-x)=2(180-x) \\ \\ 1080-12x=360-2x \\ \\ 1080-360=10x \\ \\ 720=10x \\ \\ x=72`

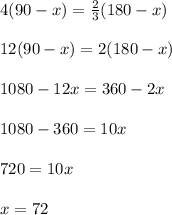
So the measure of angle will be 72°