Question

Suppose the number of dropped footballs for a wide receiver, over the course of a season, are normally distributed with a mean of 16 and a standard deviation of 2.

What is the z-score for a wide receiver who dropped 13 footballs over the course of a season?




−3

−1.5

1.5

3

Answer 1

the z-score for a wide receiver who dropped 13 footballs over the course of a season is:

-1.5

Step-by-step explanation:

The z-score is a measurement of relationship between the score and the mean of group of scores.

The formula to find the z-score is given by:

`z=(x-m)/(\sigma)`

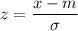
where m represent the mean score and σdenote the standard deviation.

and x is the score whose z-score is to be calculated.

Hence, here we have:

m=16 , σ=2 and x=13

Hence, the z-score is calculated as:

`z=(13-16)/(2)\\\\\\z=(-3)/(2)\\\\\\z=-1.5`

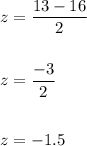
Hence, the required z-score is:

-1.5

Answer 2

Answer:
The z-score would be -1.5.

Step-by-step explanation:
The z-score shows how many standard deviations the number is from the mean.
So to find this answer you start by finding how far the number is from the mean.
13-16 = -3. So, the number is 3 less than the mean,

Then you must find how many standard deviations that is away.
So, to find this you must divide by the standard deviation.
z-score =
`(-3)/(2)` = -1.5.