Question

PLEASE HELP EASY ALGEBRA

What is the sum of the geometric sequence 1, 3, 9, … if there are 10 terms?
A: 29,524
B: 55,987
C: 87,381
D: 88,573

Answer 1

The terms of the geometric sequence are 1,3,9, ...,

The first term is a = 1
The common ratio is r = 3.

The sum of the first 10 terms is


Answer: 29524

Answer 2

Answer: Option 'A' is correct.

Explanation:

Since we have given that

Geometric series is as follows:

1,3,9,................

Number of terms = 10

n = 10

a = 1

r =
`(a_2)/(a_1)=(3)/(1)=3`

We need to find the sum of the geometric sequence for 10 terms.

`S_(10)=(a(r^n-1)/(r-1)\\\\S_(10)=(1(3^(10)-1))/(3-1)\\\\S_(10)=(59048)/(2)\\\\S_(10)=29,524`

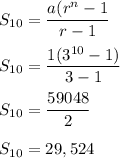
Hence, Option 'A' is correct.