Question

What is true about the solutions of a quadratic equation when the radicand in the quadratic formula is negative? No real solutions Two identical rational solutions Two different rational solutions Two irrational solutions

Answer 1

If the radicand in the quadratic formula is negative then no real solutions possible.

Explanation:

Given that when the radicand in the quadratic formula is negative then we have to find the true statement about the solution of quadratic equation.

Radicand of quadratic formula i.e the discriminant of quadratic formula.

`D=b^2-4ac`

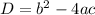
which comes in the solution under the root.

The solution of general quadratic equation is

`x=(-b\pm \sqrt D)/(2a)`

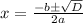
As discriminant is negative then we can not find any real root for the given equation.

Hence, option 1 is correct.

No real solutions possible.

Answer 2

The answer is
no real solutions. <<<< answer.

To confirm this, the question is saying what is the square root of (say) - 5?
There is no answer in the real number system.