Question

Diana guesses that their are120 gum balls in a jar. There are actually 96. In another game she guesses that there are 75 jelly beans in a jar. There are actually 60. In which game did Diana have the smallest percent error?

Answer 1

It would have to be the second game.

Answer 2

Diana have the same error percent in both games.

Explanation:

We have been given that Diana guesses that their are 120 gum balls in a jar. There are actually 96. In another game she guesses that there are 75 jelly beans in a jar. There are actually 60.

Let us find error percent for each scenario.

`\text{Error percent}=\frac{| \text{Approx-Exact}|}{\text{Exact}}* 100\%`

`\text{Error percent in 1st game}=(|120-96|)/(96)* 100\%`

`\text{Error percent in 1st game}=(|24|)/(96)* 100\%`

`\text{Error percent in 1st game}=(24)/(96)* 100\%`

`\text{Error percent in 1st game}=0.25* 100\%`

`\text{Error percent in 1st game}=25\%`

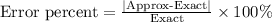
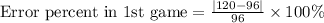
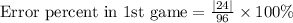
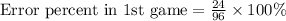
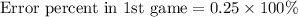
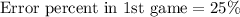
Now, we will find error percent in 2nd game.

`\text{Error percent in 2nd game}=(|75-60|)/(60)* 100\%`

`\text{Error percent in 2nd game}=(|15|)/(60)* 100\%`

`\text{Error percent in 2nd game}=(15)/(60)* 100\%`

`\text{Error percent in 2nd game}=0.25* 100\%`

`\text{Error percent in 2nd game}=25\%`

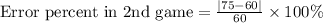
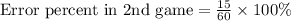
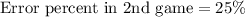
Since error percent of both games in 25%, therefore, Diana have the same error percent in both games.