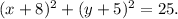Question

If the endpoints of the diameter of a circle are (−10, −8) and (−6, −2), what is the standard form equation of the circle?

Answer 1

(x+8)²+(y+5)²=52




HOPE THIS HELPED!!!!!!!!!

Answer 2

Answer: The standard form equation of the given circle is

`(x+8)^2+(y+5)^2=25.`

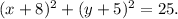
Step-by-step explanation: Given that the co-ordinates of the end-points of the diameter of a circle are (−10, −8) and (−6, −2).

We are to find the equation of the circle in standard form.

The mid-points of the diameter of a circle is the center of the circle.

So, the co-ordinates of the center of the circle are

`(h,k)\\\\=\left((-10-6)/(2),(-8-2)/(2)\right)\\\\\\=\left((-16)/(2),(-10)/(2)\right)\\\\=(-8,-5).`

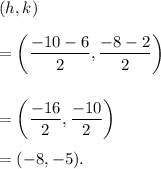
Also, the length of the radius is equal to half of the length of the diameter of the circle.

So, the length of the radius is calculate using distance formula as follows:

`r\\\\\\=(1)/(2)√((-6+10)^2+(-2+8)^2)\\\\\\=(1)/(2)√(4^2+6^2)\\\\\\=(1)/(2)√(100)\\\\\\=(1)/(2)*10\\\\\\=5.`

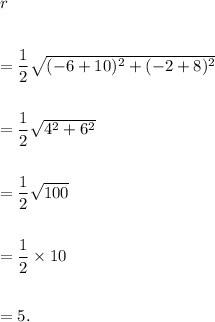
Now, the standard equation of a circle with radius r units and center at (h, k) is given by

`(x-h)^2+(y-k)^2=r^2.`

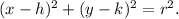
We have

center, (h, k) = (-8, -5) and radius, r = 5 units.

Therefore, the standard equation of the circle is

`\{x-(-8)\}^2+\{y-(-5)\}^2=5^2\\\\\Rightarrow (x+8)^2+(y+5)^2=25.`

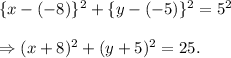
Thus, the standard form equation of the given circle is

`(x+8)^2+(y+5)^2=25.`