Question

Isaac has 21 green marbles and 7 blue marbles. He wants to place them in identical groups without any marbles left over. What is the greatest number of groups Isaac can make? PLEASE ANSWER WITH WORK!!!

Answer 1

itll be 3 groups because 21/7=3

Answer 2

7 groups.

Explanation:

We have been given that Isaac has 21 green marbles and 7 blue marbles. He wants to place them in identical groups without any marbles left over.

To find the greatest number of groups Issac can make we will find the GCF of 7 and 21.

Factors of 7 are: 1, 7.

Factors of 21 are: 1, 7, 3, 21.

We can see that 7 is the greatest common factor of 7 and 21, therefore, Issac can make 7 groups from 21 green marbles and 7 blue marbles.

Let us find number of each type of marble is each group.

`\text{Number of green marbles in each group}=(21)/(7)`

`\text{Number of green marbles in each group}=3`

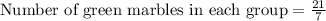
Therefore, there will be 3 green marbles in each group.

`\text{Number of blue marbles in each group}=(7)/(7)`

`\text{Number of blue marbles in each group}=1`

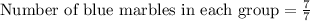
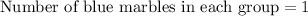
Therefore, there will be 1 blue marble in each group.