Question

The volume of a cylindrical tank is 2,916 p cubic inches and its height is 36 inches. a) What is the radius of the tank? b) What is the surface area of the tank? Give your answer in terms of p .

please help me !!

Answer 1

Volume of a Cylinder is defined by: V = Bh where B = the area of the base of the cylinder(area of the circular bottom and top), and h = the distance between the top circle and bottom circle of the cylinder.

To find the radius, we substitute the given information into the formula and solve for "r".

`2916= \pi ( r^(2) )(36)`

`(2916)/(36 \pi ) = r^(2)`

`(81)/( \pi ) = r^(2)`

`(9)/( √( \pi ) ) = r`

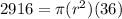
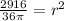
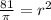
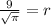
Now, to find the surface area of the tank use S.A. = 2B + π · d · h where B = the area of the circular base, d = the diameter of the circular base, and h = the height of the cylinder.


`SA = 2 \pi ( (9)/( √( \pi ) )) ^(2) + \pi ( (18)/( √( \pi ) ))(36)`

`image`
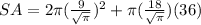
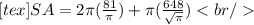
Now simplifying the first term of the expression on the right and rationalizing the denominator of the second term we get:

`image`

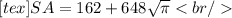
Hopefully this helps.. let me know if you have questions.