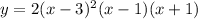Question

Which equation represents the polynomial function with zeros −1, 1, and 3 (multiplicity of 2), and a y-intercept of −18? (4 points)

y = 2(x + 3)2(x − 1)(x + 1)

y = −2(x − 3)2(x − 1)(x + 1)

y = 2(x − 3)2(x − 1)(x + 1)

y = −2(x + 3)(x − 1)(x + 1)

Answer 1

Correct Answer:
3rd option is the correct answer

Solution:
The zeros of the polynomial are -1,1 and 3. The multiplicity of 3 is 2. So the polynomial can be expressed as:


`y=a (x-3)^(2)(x-1)(x+1)`

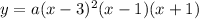
The y-intercept of the polynomial is -18. This means the polynomial passes through the point (0,-18). Therefore, y must be -18 when x = 0. Using these values of x and y in previous equation we get:


`-18=a (0-3)^(2)(0-1)(0+1) \\ \\ -18=-9a \\ \\ a=2`

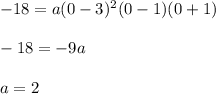
The final equation of the polynomial becomes:


`y=2 (x-3)^(2)(x-1)(x+1)`