Question

For the Transformation T, write the T^-1.

T : (x, y) (5x, 5y )
T^ -1 (x, y)

(x - 5, y - 5)
(5x - 1, 5y - 1)
(1/5x, 1/5y)

Answer 1

Answer: The correct option is

(C)
`T^(-1)(x,y)\rightarrow \left((1)/(5)x,(1)/(5)y\right).`

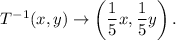
Step-by-step explanation: We are given a transformation T defined as :

`T:(x,y)\rightarrow (5x,5y).`

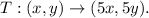
We are to find the inverse transformation
`T^(-1)(x,y).`

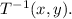
From the given transformation, we have

`T:(x,y)\rightarrow (5x,5y)\\\\\Rightarrow T^(-1)(5x,5y)=(x,y).`

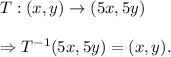
Let us consider that

`5x=z~~~~~~\Rightarrow x=(z)/(5),\\\\\\5y=t~~~~~~\Rightarrow y=(t)/(5).`

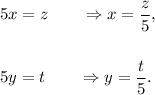
Therefore, we get

`T^(-1)(5x,5y)\rightarrow(x,y)\\\\\Rightarrow T^(-1)(z,t)\rightarrow \left((z)/(5),(t)/(5)\right)\\\\\\\Rightarrow T^(-1)(x,y)\rightarrow \left((1)/(5)x,(1)/(5)y\right).`

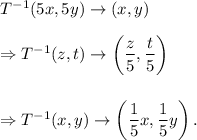
Thus, (C) is the correct option.

Answer 2

The 3rd selection is appropriate.

___
(1/5)(5x) = x, so the inverse transformation returns the original. Not so for the other choices.