Answer:
15 feet
Explanation:
Given : In this fulcrum, the weights are perfectly balanced.
To Find: How far must the fulcrum be located from the 60 pound weight if the bar is 24 feet long?
Solution:
To make the weights perfectly balanced torque must be equal
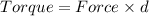
Where

Let a be the acceleration
d= Distance between the pivot and the acting point.
Let x be the distance from 60 pound weight where fulcrum is located
Since we are given that Length of bar = 24 feet.
So,Distance of fulcrum from 100 pound weight = 24-x
Now torque for 60 pound weight :

Now torque for 100 pound weight.

Now to maintain the equilibrium i.e. To make the weights perfectly balanced

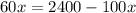
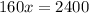

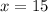
Hence The fulcrum must be located 15 feet from the 60 pound weight if the bar is 24 feet long.