Question

Suppose you can factor x^2 +bx +c as (x+p)(x+q) . If c<0, what could be the possible values of p and q?

A: p= -3, q= 7

B: p= 11, q= 4

C: p= -2, q= -5

D: p= 1, q= 10

Answer 1

What you should know is that the value of c will be given by the following product:
c = p * q
So that c <0
We have that the possible values are:
p = -3
q = 7
Thus, the value of c is:
c = p * q
c = (- 3) * (7)
c = -21 <0
Answer:
the possible values of p and q could be
A: p = -3, q = 7

Answer 2

Ans: Option A

Step-by-step explanation:
Let's solve it smartly!

Given expression:
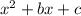
`x^(2) + bx +c` --- (A)
Factors: (x+p)(x+q)

Condition: c<0

Now let us expand (x+p)(x+q):
=>
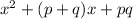
`x^(2) + (p+q)x + pq` --- (B)

By comparing (B) with (A), we can say that:

pq = c --- (C)

Now, as the condition says, c<0, it means either p or q is negative. Both cannot be positive or both cannot be negative.

1) If p>0, q>0, it means c>0 since (+p)(+q) = (+c)(according to equation (C)). Condition is not met.
Hence, option B and D are wrong.

2) If p<0, q<0 it means c>=0 since (-p)(-q) = (+c)(according to equation (C)). Condition is not met.
Hence option C is out as well.


We are left with Option A:
p<0, q>0 it means c<0 since (-p)(+q) = (-c)(according to equation (C)). Condition is MET!
Hence,
Ans: Option A: p= -3, q= 7