Question

A farmer in china discovers a mammal hide that contains 54% of its original amount of c-14. Find the age of the mammal hide to the nearest year

Answer 1

6163.2 years

Explanation:

The formula we use for evaluating the C 14 decay is

`A_t=A_0e^(-kt)`

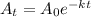
Where

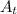`A_t`=Amount of C 14 after “t” year

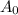`A_0`= Initial Amount

t= No. of years

k=constant

In our problem we are given that
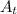`A_t` is 54% that is if
`A_0=1` ,
`A_t=0.54`

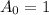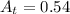
Also , k=0.0001

We have to find t=?

Let us substitute these values in the formula

`0.54=1* e^(-0.0001t)`

Taking log on both sides to the base 10 we get

`log 0.54=log e^(-0.0001t)`

`-0.267606 = -0.0001t*log e`

`-0.267606 = -0.0001t*0.4342`

`t=(-0.267606)/(-0.0001*0.4342)`

`t=6163.20`

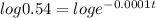
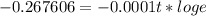
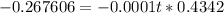
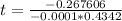
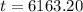
t=6163.20 years