Question

Find the solution of the differential equation that satisfies the given initial condition. y' tan x = 5a + y, y(π/3) = 5a, 0 < x < π/2, where a is a constant.

Answer 1

The other person's answer is almost correct but isnt.

It should be:

`y=(20a/√(3))sin(x)-5a`

Answer 2

`y' \tan x = 5a + y \\ \\ \indent y' \tan x - 5a = y \\ \\ \indent (y' \tan x)/(\tan x) - (5a)/(\tan x) = (y)/(\tan x) \\ \\ \indent y' - 5a\cot x = y\cot x \\ \\ \indent \boxed{y' - y\cot x = 5a\cot x} \text{ (1)}`

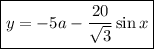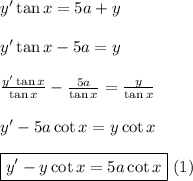
Note that the above equation is a first order non-homogeneous linear differential equation which is of the form


`y' + A(x)y = B(x)`

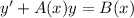
where (in the problem):


`A(x) = -\cot x \\ B(x) = 5a\cot x`

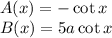
We can solve this equation by multiplying both sides by the integrating factor I(x) which is calculated as


`I(x) = e^{\int {A(x)dx}} \\ \indent = e^{\int {-\cot x dx}} \\ \indent = e^(-\ln (\sin x) + C_0) \\ \indent = e^((-1)(\ln (\sin x)) + C_0) \\ \indent = e^(C_0)\left (e^(\ln (\sin x)) \right )^(-1) \\ \indent = e^(C_0)\left (\sin x \right )^(-1) \\ \indent = e^(C_0)\left (\csc x \right ) \\ \indent \boxed{I(x) = K\csc x, K = e^(C_0)}`

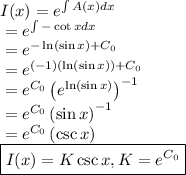
Multiplying this integrating factor to both sides of equation (1), we have


`y' - y\cot x = 5a\cot x \\ \indent K\csc x \left ( y' - y\cot x \right ) = K\csc x \left (5a\cot x \right ) \\ \indent \csc x \left ( y' - y\cot x \right ) = \csc x \left (5a\cot x \right ) \\ \indent \boxed{y'\csc x - y\csc x\cot x = 5a\csc x \cot x} \text{ (2)}`

Note that


`\boxed{y'\csc x - y\csc x\cot x = (d)/(dx)\left (y\csc x \right )}`

Using this information for equation (2),


`(d)/(dx)\left (y\csc x \right ) = 5a\csc x \cot x \\ \\ \indent y\csc x = \int {5a\csc x \cot x dx} \\ \\ \indent y\csc x = \int {5a \left ( (1)/(\sin x) \right )\left ( (\cos x)/(\sin x) \right ) dx} \\ \\ \indent \boxed{y\csc x = \int {5a \left ( (\cos x)/(\sin^2 x) \right ) dx}}\text{ (3)}`

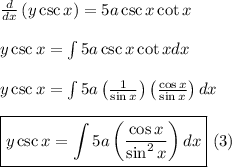
Now, we evaluate the integral on the left side. Let
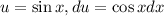
`u = \sin x, du = \cos x dx` so that


`\int {5a\left ((\cos x)/(\sin^2 x) \right ) dx} = \int {(5a)/(u^2)}du \\ \\ \indent = -(5a)/(u) + C \\ \\ \indent = -(5a)/(\sin x) + C \\ \\ \indent \boxed{\int {5a\left ( (\cos x)/(\sin^2 x) \right ) dx} = -5a\csc x + C} \text{ (4)}`

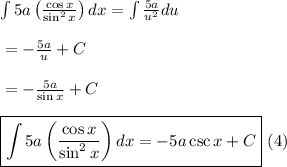
Using equation (4), equation (3) becomes


`y\csc x = -5a\csc x + C \\ \\ \indent (y\csc x)/(\csc x) = (-5a\csc x)/(\csc x) + (C)/(\csc x) \\ \\ \indent \boxed{y = -5a + C\sin x} \text{ (5)}`

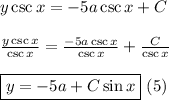
Since
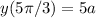
`y(5\pi /3) = 5a`, equation (5) becomes


`y(5\pi /3) = -5a + C\sin (5\pi /3) \\ \\ 5a = -5a + C \left ( -(√(3))/(2) \right ) \\ \\ C \left ( -(√(3))/(2) \right ) = 10a \\ \\ \boxed{C = -(20)/(√(3))}`

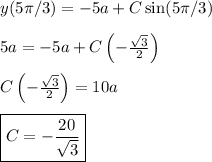
Using this value of the constant, therefore


`\boxed{y = -5a - (20)/(√(3))\sin x}`