Question

How many times greater is the rate of effusion of molecular fluorine than that of molecular bromine at the same temperature and pressure?

Answer 1

Answer: The rate of diffusion of fluorine is 2.05 times to that of bromine.

Explanation:

To calculate the rate of effusion of gas, we use Graham's Law.

This law states that the rate of effusion of gas is inversely proportional to the square root of the molar mass of the gas. The equation given by this law follows:

`\text{Rate of diffusion}\propto \frac{1}{\sqrt{\text{Molar mass of the gas}}}`

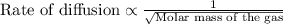
Molar mass of bromine = 160 g/mol

Molar mass of fluorine = 38 g/mol

For the rate of effusion of bromine to fluorine we write the expression:

`(Rate_(F_2))/(Rate_(Br_2))=\sqrt{(M_(Br_2))/(M_(F_2))}`

`(Rate_(F_2))/(Rate_(Br_2))=\sqrt{(160)/(38)}=2.05`

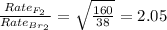
Hence, the rate of diffusion of fluorine is 2.05 times to that of bromine.

Answer 2

According to Graham's law the rates of effusion of two gases are inversely proportional to the square roots of their molar masses at the same temperature and pressure: Effusion is used to describe the passage of a gas through a tiny office into an evacuated chamber.
Therefore;, R1/R2= √mm2/√mm1
The molecular mass of fluorine is 38 g and that of 160 g
Therefore; = √ (160/38)
= √ 4.211
= 2.051
Hence; the rate of effusion of molecular fluorine is 2.051 times than that of molecular bromine at the same temperature and pressure.