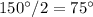The situation is shown in the figure attached.
The original beam of light comes from 12 o'clock, and it is reflected to 5 o'clock.
Since there are 12 hours on the clock, each hour covers an angle of
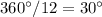
.
This means that between 12 o'clock and 5 o'clock there is an angle of
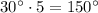
.
This corresponds to the total angle between the incident beam and the reflected beam. But for the law of reflection, we have that the incident angle should be equal to the angle of reflection, so this is only possible if both angles are half of
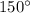
, so we have:
- angle of incidence:
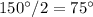
- angle of reflection: