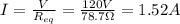Question

Two appliances are connected in parallel to a 120-v battery and draw currents i1 = 3.0 a and i2 = 3.1

a. if these appliances are instead connected in series to the same battery, what is the total current in the circuit?

Answer 1

Initially they are connected in parallel, so they have the same voltage V=120 V at their ends. Therefore we can use Ohm's law to calculate the resistance of each appliance:

`R_1 = (V)/(I_1)= (120 V)/(3.0 A)=40 \Omega`

`R_2 = (V)/(I_2)= (120 V)/(3.1 A)=38.7 \Omega`

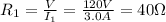
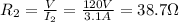
When they are connected in series, they are crossed by the same current I. The equivalent resistance of the circuit in this case is
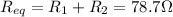
`R_(eq)=R_1+R_2 = 78.7 \Omega`, so we can use Ohm's law for the entire circuit to find the current in the circuit:

`I= (V)/(R_(eq))= (120 V)/(78.7 \Omega)=1.52 A`