Question

How much energy (in kj) do 3.0 moles of photons, all with a wavelength of 670 nm, contain? how much energy (in kj) do 3.0 moles of photons, all with a wavelength of 670 nm, contain? 360 kj 179 kj 536 kj 242 kj 412 kj?

Answer 1

1 mole of photons contain
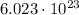
`6.023 \cdot 10^(23)` photons (Avogadro number). This means that 3.0 moles of photons contain

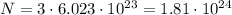
`N=3\cdot 6.023 \cdot 10^(23) =1.81 \cdot 10^(24)` photons.

The wavelength of the light in the problem is
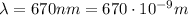
`\lambda=670 nm=670\cdot 10^(-9)m`, so the frequency is

`f= (c)/(\lambda)= (3\cdot 10^8 m/s)/(670 \cdot 10^(-9)m)=4.48 \cdot 10^(14)Hz`

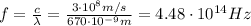
The energy carried by a single photon is

`E=hf`
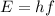
where
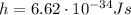
`h=6.62 \cdot 10^(-34)Js` is the Planck constant, while f is the frequency. Since this is the energy carried by a single photon, the energy carried by 3.0 moles of photons will be the energy of the single photon multiplied by the total number of photons:

`E=Nhf=(1.81 \cdot 10^(24))(6.62 \cdot 10^(-34)Js)(4.48 \cdot 10^(14)Hz )=5.36 \cdot 10^5 J`
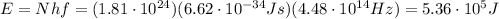
which corresponds to E=536 kJ.