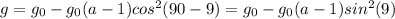Question

On a certain planet, which is perfectly spherically symmetric, the free-fall acceleration has magnitude g = go at the north pole and g = ago at the equator (with 0 < a < 1). find g(9), the freefall acceleration at colatitude 9 as a function of 9.

Answer 1

The reason why there is a difference between free-fall acceleration is a centrifugal force.
I attached a diagram that shows how this force aligns with the force of gravity.
From the diagram we can see that:

`F=F_g-F_(cf)=mg'-mw^2r'cos(\alpha)\\ ma=mg'-mw^2r'cos(\alpha)\\ a=g'-w^2rcos^2(\alpha)\\`
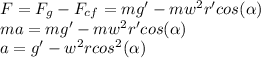
Where g' is the free-fall acceleration when there is no centrifugal force, r is the radius of the planet, and w is angular frequency of planet's rotation.
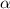
`\alpha` is the latitude.
We can calculate g' and wr^2 from the given conditions in the problem.

`g(90)=g_0;\ g_0= g'-w^2rcos^2(90)\\ g_0=g'\\ g(0)=ag_0;\ ag_0=g_0-w^2rcos^2(0)\\ ag_0=g_0-w^2r\\ w^2r=g_0(a-1)`
Our final equation is:

`g=g_0-g_0(a-1)cos^2(\alpha)`
Colatitude is:

`\alpha_c=90^\circ-\alpha`
The answer is:

`g=g_0-g_0(a-1)cos^2(90-9)=g_0-g_0(a-1)sin^2(9)`