a(i). Since you are given a velocity v. time graph, the distance will be represented by:
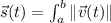
In this case, however, we can just use simple geometry to evaluate the area under the graph v(t). I split it up into 2 trapezoids, and 1 rectangle. So, the area will be as follows:
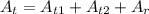
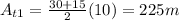
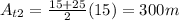
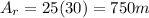
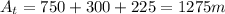
So, the particle traveled a total of
1275m assuming it never turned back (because it says to calculate distance).
a(iii). Deceleration is a word for negative acceleration. Acceleration is the first derivative of velocity, and so deceleration is too. So, we just need to find the slope of the line that passes through t = 30 because it has a linear slope (meaning the slope doesn't change). So, we can just use simple algebra instead of calculus to figure this out. Recall from algebra that slope (m):
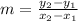
So, let's just pick values. I'm going to pick (25, 30) and (35, 15). Let's plug and chug:
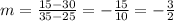
Since it's a negative value, this means that acceleration is negative but deceleration is positive (because deceleration is negative acceleration). So, your answer is:
The deceleration of the particle at t = 30s is 3/2 or 1.5.