Question

A metal cube, 2.00cm on each side, has a density of 6600 kg/m3. find its apparent weight when it is totally submerged in water.

Answer 1

Answer: 0.439488 N

Step-by-step explanation:

The apparent weight of the metal is computed as

apparent weight = weight - weight of the displaced fluid

To compute the weight of the metal, we use the following formula:


`\text{weight} = \rho gV`

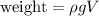
where


`\rho = \text{density of the metal = 6,600 kg/m}^3`

`g = \text{gravitational acceleration = 9.81 m/s}^2`

`V = \text{volume of the metal}`

Note that the volume is unknown but we can compute this because the metal is a cube with edge = 2 cm = 0.02 m. So, the volume of the metal is given by


`\text{Volume} = \text{edge}^3 \\ = (0.02)^3 \\ \boxed{\text{Volume = 0.000008 m} ^3}`

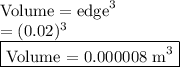
Thus, the weight of the metal is computed as


`\text{weight} = \rho gV \\ = (\text{6,600 kg/m}^3)(\text{9.81 m/s}^2)(\text{0.000008 m}^3) \\ = \text{0.517968 kg \(\cdot \) m/s}^2 \\ \boxed{\text{weight of the metal} = \text{0.517968 N}}`

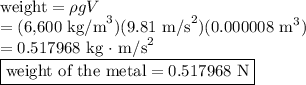
Next, we compute the displaced weight or buoyancy, which has the following formula


`\text{weight of the displaced fluid} = \rho' gV'`

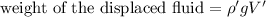
where


`\rho' = \text{density of the fluid (water) = 1,000 kg/m}^3 \\ g = \text{gravitational acceleration = 9.81 m/s}^2 \\ V' = \text{displaced volume}`

Note that the displaced volume is equal to the volume of the submerged metal. Since the metal has a volume of
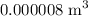
`\text{0.000008 m} ^3`, the displaced volume is
`\text{0.000008 m} ^3`.

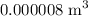
Thus, the weight of the displaced fluid is calculated as


`\text{weight of the displaced fluid} = \rho' gV' \\ = (\text{1,000 kg/m}^3)(\text{9.81 m/s}^2)(\text{0.000008 m}^3) \\ = \text{0.07848 kg \(\cdot \) m/s}^2 \\ \boxed{\text{weight of the displaced fluid} = \text{0.07848 N}}`

Therefore,

apparent weight of the metal
= weight of the metal - weight of the displaced fluid
= 0.517968 N - 0.07848 N
apparent weight of the metal = 0.439488 N