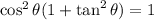Answer:
The simplified form of the expression is
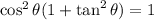
Explanation:
Given : Expression
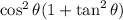
To find : The simplification of the expression?
Solution :
Step 1 - Write the expression
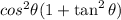
Step 2 - Using the trigonometric property,
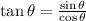
Substitute in place of
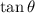
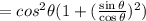
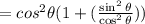
Step 3 - Taking LCM,
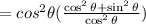
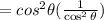
Step 4 - Cancel the term
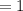
Therefore, The simplified form of the expression is