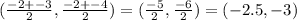Question

Quadrilateral JKLM has vertices J(–7, –2), K(–2, –2), L(–3, –4), and M(–6, –4). Find the midpoints of each of the sides JM andKL.

Answer 1

To find the midpoint of a segment (or the midpoint between two points - here the endpoints of the side) we use the midpoint formula. What it comes down to is finding the "average" of the x-coordinate and the "average" of the y-coordinate.

The formula is as follows. The midpoint of the segment with endpoints
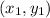
`(x_(1) ,y_(1))` and
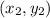
`(x_(2) ,y_(2))` is given by
`( (x_1+x_2)/(2),(y_1+y_2)/(2))`

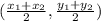
Let us find the midpoint of side JM. It does not matter which point we designate with the 1s and which we designate with the 2s so let's let J (-7,2) =
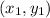
`(x_(1) ,y_(1))` and M (-6,-4) =
`(x_(2) ,y_(2))`.

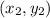
Now we plug these into the formula as follows:
`( (-7+-6)/(2),(-2+-4)/(2)) = ( (-13)/(2),(-6)/(2))=(-6.5,-3)`

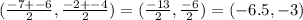
Let us now find the midpoint of side KL. It does not matter which point we designate with the 1s and which we designate with the 2s so let's let K (-2,-2) =
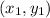
`(x_(1) ,y_(1))` and L (-3,-4) =
`(x_(2) ,y_(2))`

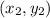
Now we plug these into the formula as follows:
`( (-2+-3)/(2),(-2+-4)/(2)) = ( (-5)/(2),(-6)/(2))=(-2.5,-3)`

Answer 2

We calculate the midpoint by taking the average of the x- and y-coordinates of both points. For side JM, with point J(-7, -2) and point M(-6, -4), we average the x-coordinates to get (-7 - 6) / 2= -13/2, and the y-coordinates average to (-2 - 4) / 2 = -3. So the midpoint of side JM is (-13/2, -3).
The calculation is similar for side KL: (-2 - 3) / 2 = -5/2, and (-2 - 4) / 2 = -3, so the midpoint of side KL is (-5/2, -3).