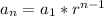Answer:
recursive formula =
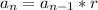
explicit formula:
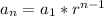
Explanation:
Thinking process:
Let a sequence be given as:
3 9 27 81
As can be observed from the sequence, the next number of the sequence is a multiple of 3, that is 9 is a multiple of 3. Similarly, 27 is 9 multiplied by 3
then, let the first term be a. the common multiplying factor will be r (in this case 3). Then the formula will be
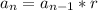
In addition, the powers rule applies.
For instance:
9 =

27 =
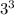
81 =

Then the explicit formula will be