Question

What is the value of x in the diagram below?

Answer 1

Answer: B

Step-by-step explanation: EDGE 2022

Answer 2

Hi,
The answer will be
`( 18√(2) )/( √(3) )` .

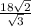
Now how is that, there is a rule for the right angled triangle which says:

cosθ =
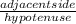
`(adjacent side)/(hypotenuse)` so, if we applied this rule on the lower triangle we can say: cos30°=
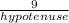
`(9)/(hypotenuse)` and therefore the hypotenuse =
`(9)/(cos30)` =
`(18)/( √(3) )` .

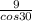
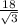
now in the upper triangle we will apply the same rule so,
cos45°=
`(adjacent side)/(hypotenuse)`
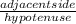
and the adjacent side in the upper triangle is
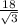
`(18)/( √(3) )` and the hypotenuse is x.
so cos45°=
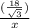
`(( (18)/( √(3) ) ))/(x)` and then we can say
x=
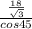
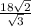
`( (18)/( √(3) ) )/(cos45)` =
`( 18√(2) )/( √(3) )` .