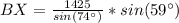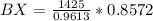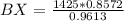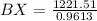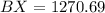Question

Ships a and b or 1425 feet apart and detect a submarine below them

Answer 1

first answer: 1084.20

second answer: 1270.69

Explanation:

correct on edge 2021

Answer 2

`AX = 1084.20`

`BX = 1270.69`

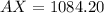
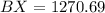
Explanation:

See attachment for complete question

Let the position of the submarine be represented with X

Given

`AB = 1425`

`\angle A = 59^(\circ)`

`\angle B = 47^(\circ)`

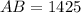
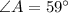
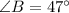
First, we calculate angle at X.

`\angle X + \angle A + \angle B = 180`

`\angle X + 59^(\circ) + 47^(\circ)= 180^(\circ)`

`\angle X = 180^(\circ) -59^(\circ) - 47^(\circ)`

`\angle X = 74^(\circ)`

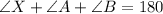
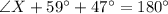
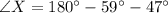
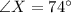
Solving (a): Distance AX: The distance between ship A and the submarine

To do this, we apply sine formula which states

`(a)/(sin\ A) = (b)/(sin\ B) = (c)/(sin\ C)`

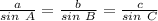
In this case:

`(AB)/(sin\ X) = (AX)/(sin\ B)`

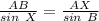
Substitute values for AB,
`\angle X` and
`\angle B`

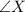`(1425)/(sin(74^(\circ))) = (AX)/(sin(47^(\circ)))`

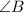
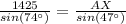
Make AX the subject

`AX = (1425)/(sin(74^(\circ))) * sin(47^(\circ))`

`AX = (1425)/(0.9613) * 0.7314`

`AX = (1425 * 0.7314)/(0.9613)`

`AX = (1042.245)/(0.9613)`

`AX = 1084.20`

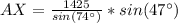
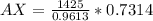
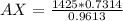
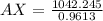
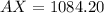
Solving (b): Distance BX: The distance between ship B and the submarine

To do this, we apply sine formula which states

In this case:

`(AB)/(sin\ X) = (BX)/(sin\ A)`

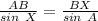
Substitute values for AB,
`\angle X` and
`\angle A`

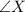`(1425)/(sin(74^(\circ))) = (BX)/(sin(59^(\circ)))`

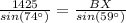
Make BX the subject

`BX = (1425)/(sin(74^(\circ))) * sin(59^(\circ))`

`BX = (1425)/(0.9613) * 0.8572`

`BX = (1425* 0.8572)/(0.9613)`

`BX = (1221.51)/(0.9613)`

`BX = 1270.69`