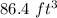Question

A prism with a base area of 5 ft² and a height of 10 ft is dilated by a factor of 6/5 . What is the volume of the dilated prism? Enter your answer, as a decimal, in the box.

Answer 1

Step
`1`

Find the volume of the original prism

we know that

the volume of the prism is equal to

`V=Bh`

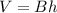
where

B is the area of the base of the prism

h is the height of the prism

in this problem we have

`B=5\ ft^(2)\\h=10\ ft`

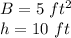
substitute in the formula of volume

`V=5*10=50\ ft^(3)`

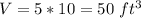
Step
`2`

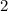
Find the volume of the dilated prism

we know that

`volume\ of\ the\ dilated\ prism=[scale\ factor^(3)]*volume\ of\ the\ original\ prism`

we have

`scale\ factor=(6)/(5)`

`volume\ of\ the\ original\ prism=50\ ft^(3)`

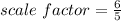
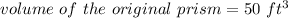
substitute the values

`volume\ of\ the\ dilated\ prism=((6)/(5))^(3)*50`

`volume\ of\ the\ dilated\ prism=1.728*50\\ \\volume\ of\ the\ dilated\ prism=86.4\ ft^(3)`

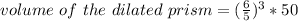
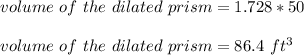
therefore

the answer is

the volume of the dilated prism is
`86.4\ ft^(3)`

Answer 2

First, you must find the original volume of the prism by applying the following formula:

V1=HxB

V1 is the original volume of the prism.
H is the height of the prism (H=10 ft).
B is the base are of the prism (B=5 ft2)

So, the original volume is:

V1=HxB
V1=(10 ft)(5 ft2)
V1=50 ft2

When the prism is dilated by a factor of 6/5, its volume is:

V2=(V1)*(6/5)^3
V2=(50 ft³)*(6/5)^3
V2= 86.4 ft³

What is the volume of the dilated prism?

The answer is: 86.4 ft³