Question

What is the ratio for the volumes of two similar cylinders, given that the ratio of their heights and radii is 3:7?

Answer 1

the answer is 27:343
Gooday

Answer 2

The ratio is
`(27)/(343)` or 27:343

Explanation:

The volume of cylinder is =
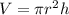`V=\pi r^(2) h` ; where r is radius and h is height.

Given that the ratio of the heights and radii of two similar cylinders is 3 : 7.

Let r' be the radius and h' be the height of the other cylinder.

Its volume is
`V'=\pi r'^(2) h'`

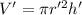
According to the given information, we have

`(r)/(r')=(h)/(h')=(3)/(7)`

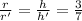
Hence, we get

`(V)/(V')=(\pi r^2h)/(\pi r'^2h')`

=
`((3)/(7))^(2) * (3)/(7)`

=
`(27)/(343)`

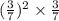
Therefore, the ratio is 27:343