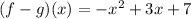Question

For f(x) = 3x +1 and g(x) = x2 – 6, find (f – g)(x).

A. x2 – 3x – 7
B. –x2 + 3x + 7
C. –x2 + 3x – 5
D. 3x2 – 17

Answer 1

Option (b) is correct.

`(f-g)(x)=-x^2+3x+7`

Step-by-step explanation:

Given : Functions
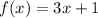`f(x) = 3x +1` and
`g(x) = x^2-6`

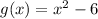
We have to choose the correct option from the given options that represents (f-g)(x)

Consider the given functions

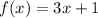`f(x) = 3x +1` and
`g(x) = x^2-6`

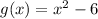
then , (f - g)(x) = f(x) - g(x)

Substitute, we have,

`f(x) - g(x)=3x+1-(x^2-6)`

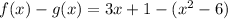
Applying plus - minus rule
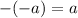`-(-a)=a`, we have,

`f(x)-g(x)=3x+1-x^2+6`

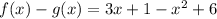
Simplify and write in standard form, we have,

`f(x)-g(x)=-x^2+3x+7`

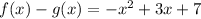
Thus, The
`(f-g)(x)=-x^2+3x+7`

Answer 2

Answer:
(f-g) (x) = -x² + 3x + 7

Step-by-step explanation:
We are given that:
f (x) = 3x + 1
g (x) = x² - 6

We want to find (f-g) (x), we can simply obtain the result by subtracting g (x) from f (x) as follows:
(f-g) (x) = f (x) - g (x)
(f-g) (x) = 3x + 1 - (x²-6)
(f-g) (x) = 3x + 1 - x² + 6
(f-g) (x) = -x² + 3x + 7

Hope this helps :)