Answer:
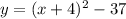
Explanation:
we know that
The equation of a vertical parabola into vertex form is equal to
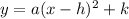
where
(h,k) is the vertex of the parabola
if a> 0 then the parabola open upward (vertex is a minimum)
if a< 0 then the parabola open downward (vertex is a maximum)
In this problem we have
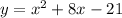
Convert to vertex form
Complete the square
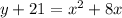

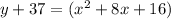
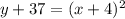
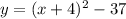 --------> equation in vertex form
--------> equation in vertex form
The vertex is the point
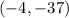
the parabola open upward (vertex is a minimum)