Question

Instructions:Select the correct answer from each drop-down menu. The sum of the squares of two consecutive positive even numbers is 340. Find the numbers. The consecutive even numbers are

Answer 1

lets name the numbers as x and x + 2
the sum of the squares of these 2 numbers are 340
x² + (x+2)² = 340
x² + x² + 4x + 4 = 340
2x² + 4x - 336 = 0
we are left with a quadratic equation
coefficient of x is 2 therefore divide each number by 2
x² + 2x - 168 = 0
to solve the quadratic equation , the 2 factors whose product is 168x² and sum is 2x is -12x and 14x
x² + 14x -12x -168 = 0
x (x + 14) - 12(x + 14)=0
(x+14)(x-12) = 0
we have 2 possible values for x
x + 14 = 0 x-12 = 0
x = -14 x = 12
from the 2 answers the correct answer is x = 12 as it should be a positive integer
one integer is 12 and consecutive even integer is 14
to check the product of the squared numbers
= 14² + 12²
= 196 + 144
= 340

Answer 2

Looking at the problem, you can come up with an equation for the consecutive numbers.


`x^(2) + (x + 2)^(2) = 340`

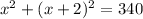
If we expand the second term:

`x^(2) + x^(2) + 4x + 4 = 340`

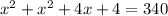
Combine like terms:


`2 x^(2) + 4x + 4 = 340`

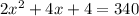
You can reduce this by dividing both sides of the equation by two:


`x^(2) + 2x + 2 = 170`

And we transpose 170 to get a standard quadratic form that the right side will be zero:

`x^(2) + 2x - 168 = 0`

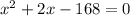
Then factor the left side:

`(x +14)(x-12) = 0`

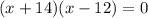
Find out the values of x that makes each factor = 0
x + 14 = 0
x = -14

We can eliminate the negative symbol because the problem is asking for positive even integers.

and;

x - 12 = 0
x = 12

Now we can say that the first positive integer is 12 and the second one is 14