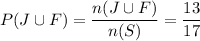Question

In a statistics class there are 11 juniors and 6 seniors; 2 of the seniors are females; 6 of the juniors are males. if a student is selected at random, what is the probability that the student is either a junior or a female?

enter your answer as a fully reduced fraction.

Answer 1

The probability is 8/17.

The tricky portion of this question is the phrasing using the word "or".
The fact that it is looking for either a female "or" a junior, let's us know that the selection can't be both. In mathematics, we would need the term "and/or" in order to include those that are both.
So, given that information, we know we have 11 juniors, 6 of which are males and 5 of which are females. We would include the males in our selection.
We also know there are 6 seniors, 2 of which are female and 4 of which are males. We would include the 2 females.

This would give us a selection size of 8. There are 17 total kids, so we divide the 8 by 17 for the answer of 8/17.

Answer 2

Answer:
`(13)/(17)`

Explanation:

Given: Number of juniors = n(J)= 11

Number of seniors = 6

Total students n(S)=
`11+6=17`

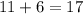
Number of seniors are which are females =2

Number of juniors are which are males =6

Then, number of juniors which are females =
`11-6=5`

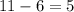
Now, total females n(F)=
`2+5=7`

such that number of juniors which are females n(J∩F) =
`5`

Now, the number of students either a junior or a female is given by :_

`n(J\cup F)=n(J)+n(F)-n(J\cap F)\\\\\Rightarrow n(J\cup F)=11+7-5=13`

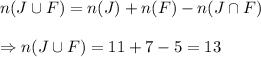
Now, the probability that the student is either a junior or a female is given by :-

`P(J\cup F)=(n(J\cup F))/(n(S))=(13)/(17)`