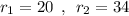Question

The equation of a circle is (x + 12)2 + (y + 16)2 = (r1)2, and the circle passes through the origin. the equation of the circle then changes to (x – 30)2 + (y – 16)2 = (r2)2, and the circle still passes through the origin. what are the values of r1 and r2?

a.r1 = 10 and r2 = 17
b.r1 = 10 and r2 = 34
c.r1 = 20 and r2 = 17
d.r1 = 20 and r2 = 34

Answer 1

d.
let x=0 and y=0,
we get
`12^2+16^2 =r _1^2`
and
`30^2+16^2 = r_2^2`
so r1=20 and r2=34

Answer 2

Option D is correct

Explanation:

Given Equations of Circles:

Circle 1 -
`(x+12)^2+(y+16)^2=(r_1)^2`

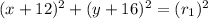
Circle 2 -
`(x-30)^2+(y-16)^2=(r_2)^2`

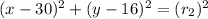
Both circles passes through origin.

To find: Values of
`r_1\:,\:r_2`

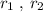
Coordinates of origin = ( 0 , 0 )

Circles passes through origin means x = 0 & y = 0 must satisfy the equation of circles.

So, Substituting x = 0 & y = 0 in Eqn of Circle 1

we get

`(0+12)^2+(0+16)^2=(r_1)^2`

`(r_1)^2=12^2+16^2`

`(r_1)^2=144+256`

`(r_1)^2=400`

`r_1=√(400)`

`r_1=20`

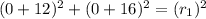
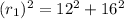
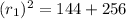
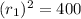
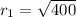
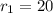
Now, Substituting x = 0 & y = 0 in Eqn of Circle 2

we get

`(0-30)^2+(0-16)^2=(r_2)^2`

`(r_2)^2=(-30)^2+(-16)^2`

`(r_2)^2=900+256`

`(r_2)^2=1156`

`r_2=√(1156)`

`r_2=34`

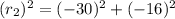
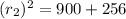
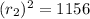
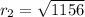
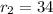
Therefore, Option D is correct .i.e.,
`r_1=20\:\:,\:\:r_2=34`