Solution :- Let X be a group of people who have received treatment for cancer ,
and t be the survival time(The number of years a person lives after receiving treatment).
Now the density function giving the distribution of t =
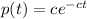
for some positive constant c.
So to know the probability of a person of the given group live not more than d days, the cumulative distribution function is given by
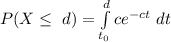 where c be any constant.
where c be any constant.
The distribution function P(t), also called the cumulative distribution function (CDF) , which tells the probability that a variate T takes a value less than or equal to a number t. And P(t)is greater than 0 and less than1