Answer:
See below.
Explanation:
Corresponding Angles Postulate
When a straight line intersects two parallel straight lines, the resulting corresponding angles are congruent.
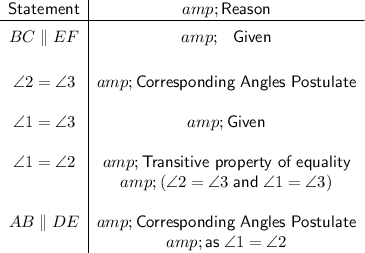
As DE intersects the two parallel lines BC and EF, ∠2 is congruent to ∠3 (corresponding angles postulate).
As ∠1 = ∠3 and ∠2 = ∠3, then ∠1 = ∠2 (transitive property of equality).
Therefore, as ∠1 and ∠2 are congruent, AB and DE must be parallel (BC is the transversal).