Question

Complete the expansion of (a + b)6 with a = 1 and b = 0.3.

(dont add everything together)
(1 + 0.3)^6  = (____

)^6  + 6(____ )^5(____) + 15(____)^4(____)^2  +  20(____)^3(____)3  + 15(____ )^2(____)^4  + 6(___ )(___)^5  + (____ )^ 6

Answer 1

`(1+0.3)^(6)=(1)^6+6(1)^(5)(0.3)+15(1)^(4)(0.3)^(2)+20(1)^(3)(0.3)^(3)+15(1)^(2)(0.3)^(4)+6(1)^(1)(0.3)^(5)+(0.3)^(6)`

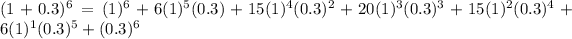
Explanation:

This is an expansion of the expression
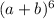`(a+b)^(6)`. In general you can expand expressions of this form by a formula known as the binomial theorem. This formula establishes that

`(a+b)^(n)=\sum_(k=0)^(n) {n\choose k} a^(n-k)b^(k)`

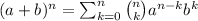
Where the coeficients
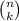`n\choose k` are called binomial coeficients, and can be computed by the formula

`{n\choose k} =(n!)/((n-k)! k!)`

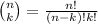
where
`n!=1* 2* 3* \cdots* n`.

Answer 2

(1+0.3)^6=(1)^6+6(1)^5(0.3)+15(1)^4(0.3)^2+20(1)^3(0.3)^3+15(1)^2(0.3)^4+6(1)(0.3)^5+(0.3)^6

(1+0.3)^6=1+6(1)(0.3)+15(1)(0.09)+20(1)(0.027)+15(1)(0.0081)+6(0.00243)+0.000729

(1+0.3)^6=1+1.8+1.35+0.54+0.1215+0.01458+0.000729