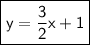Question

What is the equation, in slope-intercept form, of the line that is perpendicular to the line Y-4=-2/3(X-6) and passes through the point (-2,-2)

Answer 1

d

Explanation:

Answer 2

That line is in point-slope form:


`\sf y-y_1=m(x-x_1)`

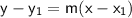
Where 'm' is the slope and (x1, y1) is a point on the line.

Perpendicular lines have opposite slopes. To get the opposite, we take the reciprocal and multiply it by -1.


`\sf -(2)/(3)`

Reciprocal:


`\sf -(3)/(2)`

Multiply by -1:


`\sf(3)/(2)`

We can plug this slope and the point into point-slope form, and then convert it to slope-intercept form.


`\sf y-y_1=m(x-x_1)`


`\sf y-(-2)=(3)/(2)(x-(-2))`

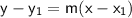
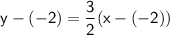
Negatives cancel out:


`\sf y+2=(3)/(2)(x+2)`

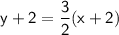
Distribute 3/2 into the parenthesis:


`\sf y+2=(3)/(2)x+(6)/(2)`

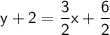
Simplify the fraction:


`\sf y+2=(3)/(2)x+3`

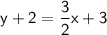
Subtract 2 to both sides:


`\boxed{\sf y=(3)/(2)x+1}`