Question

A basketball coach is purchasing 12 shirts for her team, each with a different number. At the checkout counter, the clerk places 5 of the shirts in the first bag. How many different ways can a group of 5 shirts be placed in that first bag? A. 19,008

B. 60
C. 792
D. 95,040

Answer 1

Kidjov the answer I came up with for you is 792 I hope this helps

Answer 2

Answer: Option 'C' is correct.

Explanation:

Since we have given that

Total number of shirts purchased for her team = 12

Number of shirts places in the first bag = 5

We need to find the number of ways a group of 5 shirts be placed in that first bag.

We will use "Combination" to find the number of different ways :

As we know the formula for Combination.

`^nC_r=(n!)/(r!* (n-r)!)\\\\here, n=12\\\\r=5\\\\So,\ it\ becomes,\\\\^(12)C_5=(12!)/(5!* 7!)\\\\=(12* 11* 10* 9* 8)/(5* 4* 3* 2)\\\\=792`

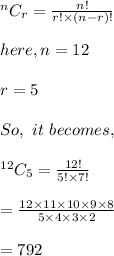
Hence, there are 792 ways to do so.

Therefore, Option 'C' is correct.