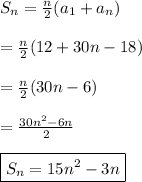Question

A statement Sn about the positive integers is given. Write statements S1, S2, and S3, and show that each of these statements is true. Show your work. Sn:   12 + 42 + 72 + . . . + (3n - 2)2 = n(6n^2-3n-1)/2

Answer 1

Answer:


`S_1 = 12 \\ S_2 = 54 \\ S_3 = 126 \\ S_n = 15n^2 - 3n`

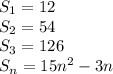
Step-by-step explanation: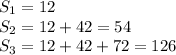


`S_1 = 12 \\ S_2 = 12 +42 = 54 \\ S_3 = 12 + 42 + 72 = 126`

To calculate for
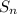
`S_n`, note that the series is an arithmetic series because each term is equal to the preceding term plus a constant, which is 30 (called common difference).

We let


`a_1 = \text{ first term} = 12 \\ a_2 = \text{ second term} = 42 \\ a_3 = \text{ third term} = 72\\. \\. \\. \\a_n = n\text{th term}`

Since
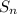
`S_n` is an arithmetic series,
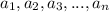
`a_1, a_2, a_3, ... , a_n` is an arithmetic sequence and so the formula for the nth term is given by


`a_n = a_1 + d(n - 1) \\ a_n = 12 + 30(n - 1) \\ \boxed{a_n = 30n - 18}`

Where d = common difference = 30

Now, since
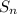
`S_n` is an arithmetic series, we can use the formula for the sum of the arithmetic series, which is given by


`S_n = (n)/(2) (a_1 + a_n) \\ \\ = (n)/(2) (12 + 30n - 18) \\ \\= (n)/(2) (30n - 6) \\ \\ = (30n^2 - 6n)/(2) \\ \\ \boxed{S_n = 15n^2 - 3n}`