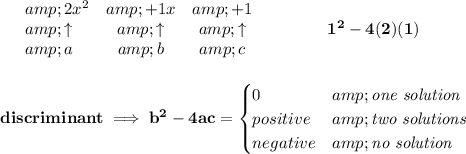Question

How would you factor

4x^3 + 2x^2 + 2x?

Please explain in steps not just give me the straight answer.

Answer 1

`\bf 4x^3+2x^2+2x\implies 2x(2x^2+x+1)`

so in short, the only factoring doable to it, without any complex factors, is that of taking the common factor of 2x.

now, the trinomial of 2x²+x+1, will not give us any "real roots", just complex or "imaginary" ones.

if you have already covered the quadratic formula, you could test with that, or you can also check that trinomial's discriminant, and notice that it will give you a negative value.


`\bf \begin{array}{llcccll} & 2 x^2& +1 x& +1\\ &\uparrow &\uparrow &\uparrow \\ &a&b&c \end{array}\qquad \qquad 1^2-4(2)(1) \\\\\\ discriminant\implies b^2-4ac= \begin{cases} 0&\textit{one solution}\\ positive&\textit{two solutions}\\ negative&\textit{no solution} \end{cases}`

Answer 2

`2x(2x^2+x+1)`

Explanation:

We have been given an expression and we are asked to find factor out our given expression.

`4x^3+2x^2+2x`

To factor our given expression we need to factor out the greatest common factor of each term of our given expression.

We can rewrite our given expression as:

`(2\cdot 2\cdot x\cdot x\cdot x)+(2x\cdot x)+2x`

We can see that the greatest common factor of our given expression is 2x.

Upon factoring out 2x from our given expression we will get,

`2x(2\cdot x\cdot x+x+1)`

`2x(2x^2+x+1)`

Therefore, the factored form of our given expression is
`2x(2x^2+x+1)` .