Question

Find the discriminant of the quadratic $3x^2 - 7x + 6.$

Answer 1

Solve for x:
3 x^2 - 7 x + 6 = 0

Divide both sides by 3:
x^2 - (7 x)/3 + 2 = 0

Subtract 2 from both sides:
x^2 - (7 x)/3 = -2

Add 49/36 to both sides:

x^2 - (7 x)/3 + 49/36 = -23/36

Write the left hand side as a square:
(x - 7/6)^2 = -23/36

Take the square root of both sides:
x - 7/6 = (i sqrt(23))/6 or x - 7/6 = -(i sqrt(23))/6

Add 7/6 to both sides:
x = 7/6 + (i sqrt(23))/6 or x - 7/6 = -(i sqrt(23))/6

Add 7/6 to both sides:

Answer: x = 7/6 + (i sqrt(23))/6 or x = 7/6 - (i sqrt(23))/6

Answer 2

Discriminant of the quadratic is-23

Explanation:

The given quadratic function is
`3x^2-7x+6`

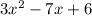
Comparing with the expression
`ax^2+bx+c`

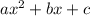
a = 3, b = -7, c = 6

The discriminant of the quadratic is given by
`D=b^2-4ac`

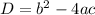
Substituting the known values, discriminant of the quadratic is

`D=(-7)^2-4(3)(6)\\\\D=49-72\\\\D=-23`

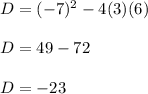
Therefore, discriminant of the quadratic is-23