Answer with Step-by-step explanation:
We are given that
Angle 2 and angle 5 are supplementary.
We have to prove that l is parallel to m.
Step 1:
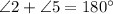
Reason:By definition of supplementary angles.]
Step 2:

Reason:Vertical angle theorem.
Step 3:
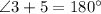
Reason : substitute property
Step 4:angle 3 and angle 5 are supplementary.
Reason: By definition of supplementary angles.
Step 5:
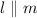
Reason:Converse of same side interior angles theorem.