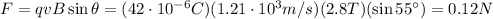Question

Particle q₁ has a charge of 2.7 μC and a velocity of 773 m/s. If it experiences a magnetic force of 5.75 × 10⁻³ N, what is the strength of the magnetic field?

A. 0.36 T
B. 1.6 T
C. 2.8 T

In the same magnetic field, particle q₂ has a charge of 42.0 μC and a velocity of 1.21 × 10³ m/s. What is the magnitude of the magnetic force exerted on particle 2?
A. 0.042 N
B. 0.12 N
C. 0.14 N

Answer 1

1. 2.8

2. 0.12

Step-by-step explanation:

Answer 2

The intensity of the magnetic force F experienced by a charge q moving with speed v in a magnetic field of intensity B is equal to

`F=qvB \sin \theta`
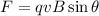
where
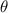
`\theta` is the angle between the directions of v and B.

1) Re-arranging the previous formula, we can calculate the value of the magnetic field intensity. The charge is
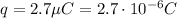
`q=2.7 \mu C=2.7 \cdot 10^(-6)C`. In this case, v and B are perpendicular, so
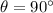
`\theta=90^(\circ)`, therefore we have:

`B= (F)/(qv \sin \theta) = (5.75 \cdot 10^(-3)N)/((2.7 \cdot 10^(-6)C)(773m/s)\sin 90^(\circ))=2.8 T`

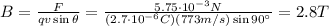
2) In this second case, the angle between v and B is
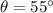
`\theta=55^(\circ)`. The charge is now
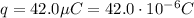
`q=42.0 \mu C=42.0 \cdot 10^(-6)C`, and the magnetic field is the one we found in the previous part, B=2.8 T, so we can find the intensity of the force experienced by this second charge:

`F=qvB \sin \theta=(42\cdot 10^(-6)C)(1.21 \cdot 10^3 m/s)(2.8 T)(\sin 55^(\circ))=0.12 N`