Question

Scarlett is trying to find the height of a dam. She stands 90 meters away from the dam and records the angle of elevation to the top of the dam to be 26º. Scarlett's height is 1.65 meters, so the height of the dam is meters. NextReset

Answer 1

the height of a dam:
h = x + 1.65 m,
where:
x = 90 m · tan 26°
x = 90 · 0.4877
x = 43.90
h = 43.90 m + 1.65 m = 45.55 m
Answer:
The height of the dam is 45.5 m.

Answer 2

The height of dam =45.5 m.

Explanation:

We are given that Scarlett stands 90 m away from the dam and records the angle of elevation to the top of the dam to be
`26^(\circ)p`

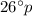
Scarelett's height is 1.65 meters.

We have to find the height of the dam.

Let h be the height of dam

AC=AB+BC

BC=x

h=1.65+x

CD=EB=90 m

In triangle ABE

`\theta=26^(\circ)`

`tan\theta=(perpendicular\;side)/(Base)`

`tan26^(\circ)=(AB)/(90)`

`0.4877=(x)/(90)`

`x=0.4877* 90`

`x=43.893 m`

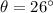
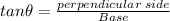
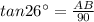
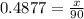
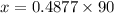
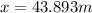
Therefore, the height of dam=1.65+43.893=45.543 m

Answer: The height of dam =45.5 m