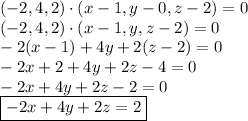Answers:
(i) 3
(ii)
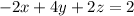
Explanation: (i) The area of the parallelogram bounded by vectors u and v is given by:
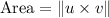
Note that if

,
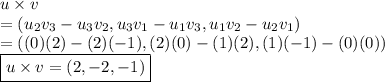
Thus, the area of the parallelogram formed by vectors u and v is calculated as
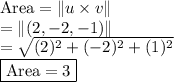
Hence, the area of the parallelogram is 3.
(ii) To obtain the equation of the plane, we must get its normal vector and a point in the plane.
As calculated in (i), the normal vector to the plane is
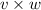
because the plane is parallel to vectors v and w. Note that if
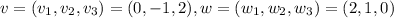
,
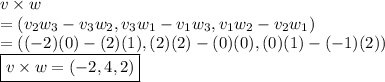
Thus, a normal vector to the plane is
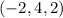
.
To get a point in the plane, note that vector u can be represented by
any pairs of points. So, we can take (0, 0, 0) to be the starting point of vector u. Since
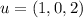
, the tip of vector u is
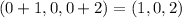
. Because the plane passes thru the tip of vector u, a point in the plane has coordinates
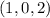
.
So for any point

in the plane, the equation is given by
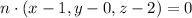
Where n is the normal vector to the plane.
Since
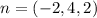
, the equation becomes