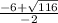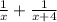
(by taking the common factor for the two elements of the equation
![\frac{1]{x} *(x+4)/(x+4) +(1)/(x+4)*(x)/(x)=(x+4)/(x*(x+4))+(x)/(x*(x+4))]()
now we can add both of the equation as the denominators have the same value.
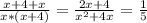
by multiplying both sides by
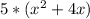
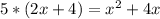
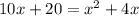
by subtracting both sides by (10x+20)
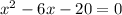
(by using the quadratic formula)
we will find two answers for this equation
x={
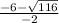
and