Question

Suppose f(x)=x^2 and g(x)=-1/5(x-3)^2. Which statement best compares the graph of g(x) with the graph of f(x)? A. The graph of G(x) is the graph of F(x) compressed vertically, flipped over the x-axis, and shifted 3 units to the right. B. The graph of G(x) is the graph F(x) compressed vertically, flipped over the x-axis , and shifted 3 units to the left. C. The graph of G(x) is the graph of F(x) stretched vertically, flipped over the x-axis , and shifted 3 units to the left. D. The graph of G(x) is the graph of F(x) stretched vertically, flipped over the x-axis, and shifted 3 units to the right.

Answer 1

The correct option is A.

Explanation:

The given functions are

`f(x)=x^2`

`g(x)=-(1)/(5)(x-3)^2`

It can be written as

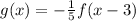`g(x)=-(1)/(5)f(x-3)` .... (1)
`[\because f(x-3)=(x-3)^2]`

The transformation is defined as

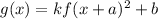`g(x)=kf(x+a)^2+b` .... (2)

Where, k is vertical stretch or compression, a is horizontal shift and b is vertical shift.

If |k|>1, then the graph stretch vertically and if 0<|k|<1, then graph compressed vertically.

If a>0, then the graph shifts a units left and if a<0, then the graph shifts a units right.

If b>0, then the graph shifts b units up and if b<0, then the graph shifts b units down.

From equation (1) and (2), we get

`k=-(1)/(5), a=-3, b=0`

Here the negative means, the graph of f(x) flipped over the x-axis.

Since 0<|k|<1, therefore the graph compressed vertically.

The value of a is -3<0, so graph shifts 3 units right.

The graph of f(x) is the graph of g(x) compressed vertically, flipped over the x-axis, and shifted 3 units to the right.

Therefore the correct option is A.

Answer 2

I'm not sure of the meaning of the word compressed. If it means that G(x) is flattened out then that is what I take compressed to mean.

The graph is compressed by the 1/5.
the graph is flipped over the x axis by the minus.
the graph is moved 3 units to the right by the - 3 inside the brackets.

A<<<< answer.