Question

The graph shows the function of f(x)=(3.5)^x

Which graph represents the function g(x)=(3.5)^x-1?

Answer 1

The one that passes through the origin. That one in the lower left part.

Answer 2

The graph of the function is the last graph.

Explanation:

To know which graph represents the function
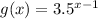`g(x)=3.5^(x-1)` you should give values to x and compare it with the values on the graphs, as follows:

When x=-3

`g(-3)=3.5^(-3-1)`

`g(-3)=3.5^(-4)`

`g(-3)=0.007`

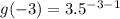
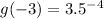
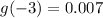
So, the first point is (-3, 0.007)

When x=-2

`g(-2)=3.5^(-2-1)`

`g(-2)=3.5^(-3)`

`g(-2)=0.02`

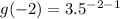
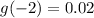
So, the second point is (-2, 0.02)

When x=-1

`g(-1)=3.5^(-1-1)`

`g(-1)=3.5^(-2)`

`g(-1)=0.08`

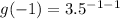
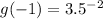
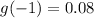
So, the third point is (-1, 0.08)

When x=0

`g(0)=3.5^(0-1)`

`g(0)=3.5^(-1)`

`g(0)=0.29`

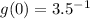
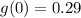
So, the fourth point is (0, 0.29)

When x=1

`g(1)=3.5^(1-1)`

`g(1)=3.5^(0)`

`g(1)=1`

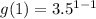
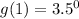
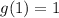
So, the fifth point is (1, 1)

When x=2

`g(2)=3.5^(2-1)`

`g(2)=3.5^(1)`

`g(2)=3.5`

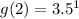
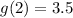
So, the fourth point is (2, 3.5)

If you compares all the points, the graph of the function is the last graph.